DASMTX Delay-And-Sum matrix

DASMTX returns a Delay-And-Sum matrix for linear beamforming.

Contents

Syntax

M = DASMTX(SIG,X,Z,DELAYS,PARAM) returns the numel(X) -by- numel(SIG) delay-and-sum DAS matrix. The matrix M can be used to beamform SIG (RF or I/Q signals) at the points specified by X and Z.

M = DASMTX(SIG,X,Z,PARAM,[X0 Z0]) assumes that the transmit originates from a virtual source located at (X0,Z0). You may prefer this syntax after using TXDELAY(X0,Z0,PARAM). This syntax is recommended for focused transmits.

TRY IT! Enter dasmtx in the command window for an example.

Because the signals in SIG are not required (only its size is needed) to create M, the following syntax is recommended:

M = DASMTX(size(SIG),X,Z,DELAYS,PARAM)

!IMPORTANT! -- With this syntax, use M = DASMTX(1i*size(SIG),...) to return a complex DAS matrix for I/Q data.

DELAYS are the transmit time delays (in s). The number of elements in DELAYS must be the number of elements in the array (which is equal to size(SIG,2)). If a sub-aperture was used during transmission, use DELAYS(i) = NaN if element # i of the linear array was off.

PARAM is a structure that contains the parameter values required for DAS beamforming (see below for details).

DASMTX versus DAS

DASMTX is also called by DAS. DASMTX thus returns the same beamformed results as DAS.

bfSIG = das(SIG,x,z,delays,param)

M = dasmtx(size(SIG),x,z,delays,param);

bfSIG = M*SIG(:);

bfSIG = reshape(bfSIG,size(x));

M is a large sparse matrix. Computing M can be much more cost-effective than using DAS if you need to beamform several SIG matrices, because M needs to be determined only once.

Let us consider that a series SIG{1}, SIG{2} ... SIG{N} of ultrasound matrices have been generated by sending similar wavefronts with the same ultrasound array. These signals SIG{i} are stacked in a 3D array sig3D so that sig3D(:,:,i) = SIG{i}. To beamform these data with a delay-and-sum approach, the following can be used.

To obtain the DAS matrix, use dasmtx:

M = dastmtx([size(sig3D,1) size(sig3D,2)],x,z,delays,param) or

M = dastmtx(1i*[size(sig3D,1) size(sig3D,2)],...) for I/Q data.

The beamformed signals are then calculated by a matrix multiplication:

bfSIG3D = M*reshape(sig3D,[],size(sig3D,3))

It is necessary to reshape the beamformed matrix array:

bfSIG3D = reshape(bfSIG3D,size(x,1),size(x,2),[])

You can also consider saving the DAS matrix M in a MAT file and loading it when needed. The previous syntax is generally much faster than:

for k = 1:N, bfSIG{k} = das(SIG{k},x,z,delays,param); end

Other syntaxes

DASMTX(SIG,X,Z,PARAM) uses DELAYS = param.TXdelay.

DASMTX(...,METHOD) specifies the interpolation method. The available methods are decribed in NOTE #3 below.

[M,PARAM] = DASMTX(...) also returns the structure PARAM with the default values.

The structure PARAM

PARAM is a structure that contains the following fields:

A note on the f-number

The f-number is defined by the ratio (depth)/(aperture size). A null f-number, i.e. PARAM.fnumber = 0, means that the full aperture is used during DAS-beamforming. This might be a suboptimal strategy since the array elements have some directivity.

Use PARAM.fnumber = [] to obtain an "optimal" f-number, which is estimated from the element directivity (and depends on fc, bandwidth, element width):

Advanced syntax for vector Doppler

PARAM.RXangle: reception angles (in rad, default = 0)

This option can be used for vector Doppler. Beamforming with at least two (sufficiently different) reception angles enables different Doppler directions and, in turn, vector Doppler.

Notes

The X axis is PARALLEL to the transducer and points from the first (leftmost) element to the last (rightmost) element (X = 0 at the CENTER of the transducer).

The Z axis is PERPENDICULAR to the transducer and points downward (Z = 0 at the level of the transducer, Z increases as depth increases). See the figure below.

For a convex array, the X axis is parallel to the chord and Z = 0 at the level of the chord.

DASMTX uses a standard delay-and-sum. It is a linear operator. Phase rotations are included if I/Q (complex) signals are beamformed.

By default DASMTX uses a linear interpolation to generate the DAS matrix. To specify the interpolation method, use DASMTX(...,METHOD), with METHOD being:

The linear interpolation (it is a 2-point method) returns a matrix twice denser than the nearest-neighbor interpolation. It is 3, 4, 5, 6 times denser for 'quadratic', 'lanczos3', '5points', 'lanczos5', respectively (they are 3-to-6-point methods).

Uniform linear array (ULA)

The pitch is defined as the center-to-center distance between two adjacent elements. The kerf width is the distance that separates two adjacent elements. They are constant for a uniform linear array (ULA).

Some functions of the MUST toolbox can also consider curved (convex) ULAs.

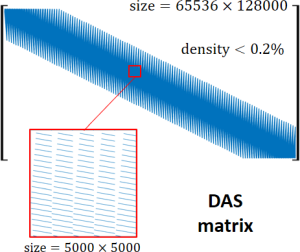
The DAS matrix

The DAS matrix is very sparse. It is complex when beamforming I/Q signals, which should be the preferred approach.

Here is an example of a DAS matrix:

Example #1: Beamform signals from a phased array

This example shows how to simulate RF signals then beamform I/Q signals

Download the properties of a 2.7-MHz 64-element cardiac phased array in a structure param by using GETPARAM.

param = getparam('P4-2v');

Calculate the transmit delays to generate a non-tilted 80-degrees wide circular wave.

width = 60/180*pi; % width angle in rad
txdel = txdelay(param,0,width); % in s

Create the scatterers of a 12-cm-by-12-cm phantom.

xs = rand(1,50000)*12e-2-6e-2;
zs = rand(1,50000)*12e-2;
idx = hypot(xs,zs-.05)<1e-2;
xs(idx) = []; % create a 1-cm-radius hole
zs(idx) = [];
RC = 3+randn(size(xs)); % reflection coefficients

Simulate RF signals by using SIMUS.

param.fs = 4*param.fc; % sampling frequency
RF = simus(xs,zs,RC,txdel,param);

Demodulate the RF signals.

IQ = rf2iq(RF,param);

Create a 256x256 80-degrees wide polar grid with IMPOLGRID.

[x,z] = impolgrid([256 256],10e-2,pi/3,param);

Create the DAS matrix.

Mdas = dasmtx(1i*size(IQ),x,z,txdel,param);
spy(Mdas(1:10000,1:10000))
title('A close up of the DAS matrix')

Beamform the I/Q signals.

IQb = Mdas*IQ(:);
IQb = reshape(IQb,size(x));

Create the ultrasound image with BMODE.

B = bmode(IQb,30); % log-compressed B-mode image with a -30 dB range

Display the ultrasound image

pcolor(x*100,z*100,B)
c = colorbar;
c.YTick = [0 255];
c.YTickLabel = {'-30 dB','0 dB'};
colormap gray
title('A simulated ultrasound image')
ylabel('[cm]')
shading interp
axis equal ij tight
set(gca,'XColor','none','box','off')

Example #2: Beamform signals from a convex array

This example shows how to simulate RF signals with a convex array and how to beamform the I/Q signals with DAS.

Download the properties of a 2.7-MHz 64-element cardiac phased array in a structure param by using GETPARAM.

param = getparam('C5-2v');

Create the scatterers of a 17-cm-by-10-cm cyst phantom.

xs = rand(1,100000)*17e-2-8.5e-2;
zs = rand(1,100000)*10e-2;
idx = hypot(xs-.02,zs-.04)<1e-2; % create a 1-cm-radius hole
xs(idx) = [];
zs(idx) = [];
RC = 3+randn(size(xs)); % reflection coefficients
idx = hypot(xs+.02,zs-.06)<1e-2; % create a 1-cm-radius cyst
RC(idx) = RC(idx)+10;

Simulate RF signals by using SIMUS.

txdel = zeros(1,128); % transmit delays
param.fs = 4*param.fc; % sampling frequency
opt.ElementSplitting = 1; % to make simulations faster
RF = simus(xs,zs,RC,txdel,param,opt);

Demodulate the RF signals.

IQ = rf2iq(RF,param);

Create a 256x256 polar grid with IMPOLGRID.

[x,z] = impolgrid([256 256],10e-2,param);

It is recommended to use an "optimal" f-number.

param.fnumber = [];

Create the DAS matrix with DASMTX.

Mdas = dasmtx(1i*size(IQ),x,z,txdel,param);

Beamform the I/Q signals.

IQb = Mdas*IQ(:);
IQb = reshape(IQb,size(x));

Create the ultrasound image with BMODE.

B = bmode(IQb,30); % log-compressed B-mode image with a -30 dB range

Display the ultrasound image

pcolor(x*100,z*100,B)
c = colorbar;
c.YTick = [0 255];
c.YTickLabel = {'-30 dB','0 dB'};
colormap gray
title('A simulated ultrasound image')
ylabel('[cm]')
shading interp
axis equal ij tight
set(gca,'XColor','none','box','off')

See also

cite, das, dasmtx3, simus, txdelay

References

About the author

Damien Garcia, Eng., Ph.D.
INSERM researcher
Creatis, University of Lyon, France

websites: BioméCardio, MUST

Date modified

Published with MATLAB® R2022a