SIMUS Simulation of ultrasound RF signals for a linear or convex array
SIMUS simulates ultrasound RF radio-frequency signals generated by an ultrasound uniform LINEAR or CONVEX array insonifying a medium of scatterers.
Contents
- Syntax
- Uniform linear array (ULA)
- The structure PARAM
- Other syntaxes
- Parallel computing
- X-, Y-, and Z-axes
- Element directivity
- Note on BAFFLE property
- Note on CHIRP signals
- Examples of pulse responses
- Advanced options
- Example #1: RF signals using a phased-array transducer
- Example #2: RF signals in plane wave imaging
- Example #3: M87-black-hole ultrasound image with diverging waves
- Example #4: Recover a few scatterers with a convex array
- See also
- References
- About the author
- Date modified
Syntax
RF = SIMUS(X,Y,Z,RC,DELAYS,PARAM) simulates ultrasound RF radio- frequency signals generated by an ultrasound uniform linear or convex array insonifying a medium of scatterers. The scatterers are characterized by their coordinates (X, Y, Z) and reflection coefficients RC.
X, Y, Z and RC must be of same size. The elements of the ULA are excited at different time delays, given by the vector DELAYS. The transmission and reception characteristics must be given in the structure PARAM (see below for details).
RF = SIMUS(X,Z,RC,DELAYS,PARAM) or RF = SIMUS(X,[],Z,RC,DELAYS,PARAM) disregards elevation focusing (PARAM.focus is ignored) and assumes that Y=0 (2-D space). The computation is faster in 2-D.
TRY IT! Enter simus in the command window for an example.
The RF output matrix contains Number_of_Elements columns. Each column therefore represents an RF signal. The number of rows depends on the depth (estimated from max(Z)) and the sampling frequency PARAM.fs (see below). By default, the sampling frequency is four times the center frequency.
Units: X, Y, Z must be in m; DELAYS must be in s; RC has no unit. RF has arbitrary unit.
DELAYS can also be a matrix. This alternative can be used to simulate MLT (multi-line transmit) sequences. In this case, each ROW represents a delay series. For example, to create a 4-MLT sequence with a 64-element phased array, DELAYS matrix must have 4 rows and 64 columns (size = [4 64]).
SIMUS uses PFIELD during transmission and reception. The parameters that must be included in the structure PARAM are similar as those in PFIELD. Additional parameters are also required (see below).
Uniform linear array (ULA)
The pitch is defined as the center-to-center distance between two adjacent elements. The kerf width is the distance that separates two adjacent elements. They are constant for a uniform linear array (ULA).
Some functions of the MUST toolbox can also consider curved (convex) ULAs.


The structure PARAM
PARAM is a structure that contains the following fields:
- TRANSDUCER PROPERTIES
- PARAM.fc: central frequency (in Hz, required)
- PARAM.pitch: pitch of the linear array (in m, required)
- PARAM.width: element width OR PARAM.kerf: kerf width (in m, required; width = pitch-kerf)
- PARAM.focus: elevation focus (in m, ignored if Y is not given). The default is Inf (no elevation focusing)
- PARAM.height: element height (in m, ignored if Y is not given). The default is Inf (no elevation focusing)
- PARAM.radius: radius of curvature (in m). The default is Inf (rectilinear array)
- PARAM.bandwidth: pulse-echo (2-way) 6dB fractional bandwidth (in %). The default is 75%.
- PARAM.baffle: property of the baffle: 'soft' (default), 'rigid' or a scalar > 0. See Note on BAFFLE property below for details.
- MEDIUM PARAMETERS
- PARAM.c: longitudinal velocity (in m/s, default = 1540 m/s)
- PARAM.attenuation: attenuation coefficient (dB/cm/MHz, default: 0). A linear frequency-dependence is assumed. A typical value for soft tissues is ~0.5 dB/cm/MHz.
- TRANSMIT PARAMETERS
- PARAM.TXapodization: transmision apodization (default: no apodization)
- PARAM.TXnow: number of wavelengths of the TX pulse (default: 1). Use PARAM.TXnow = Inf for a mono-harmonic signal.
- PARAM.TXfreqsweep: frequency sweep for a linear chirp (default: [ ]). To be used to simulate a linear TX chirp. See Note on CHIRP signals below for details.
- RECEIVE PARAMETERS (not in PFIELD)
- PARAM.fs: sampling frequency (in Hz, default = 4*param.fc).
- PARAM.RXdelay: reception law delays (in s, default = 0)
Other syntaxes
[RP,PARAM] = SIMUS(...) also returns the complete list of parameters including the default values.
[...] = SIMUS without any input argument provides an interactive example designed to produce RF signals from a focused ultrasound beam using a 2.7 MHz phased-array transducer.
Parallel computing
SIMUS calls the function PFIELD. If you have the Parallel Computing Toolbox, SIMUS can run several PFIELD functions in parallel. If this option is activated, a parallel pool is created on the default cluster. All workers in the pool are used. The X, Y and Z are split into NW chunks, NW being the number of workers. To execute parallel computing, use:
[...] = SIMUS(...,OPTIONS),
with OPTIONS.ParPool = true (default = false).
X-, Y-, and Z-axes
Conventional axes are used:
- For a LINEAR array, the X-axis is PARALLEL to the transducer and points from the first (leftmost) element to the last (rightmost) element (X = 0 at the CENTER of the transducer). The Z-axis is PERPENDICULAR to the transducer and points downward (Z = 0 at the level of the transducer, Z increases as depth increases). The Y-axis is such that the coordinates are right-handed. These axes are represented in the above ULA figure.
- For a CONVEX array, the X-axis is parallel to the chord and Z = 0 at the level of the chord.
Element directivity
By default, the calculation is made faster by assuming that the directivity of the elements is dependent only on the central frequency (see figure below). This simplification very little affects the pressure field in most situations (except in the vicinity of the array). To turn off this option, use OPTIONS.FullFrequencyDirectivity = true.
See ADVANCED OPTIONS below.
Note on BAFFLE property
In PFIELD, it is assumed by default that the array elements are embedded in an infinite SOFT baffle. To modify the property of the baffle, modify the field PARAM.baffle:
- 'rigid'
- 'soft' (this is the default)
- a nonnegative scalar
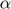 , with
, with 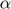 = (medium impedance)/(baffle impedance). Note:
= (medium impedance)/(baffle impedance). Note: 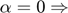 'rigid';
'rigid';  'soft'.
'soft'.

The baffle property affects the obliquity factor included in the directivity of the elements. This obliquity factor is not 1 if the baffle is not rigid. A general case (see case #3 below) can be chosen by specifying an impedance ratio. For details, refer to the corresponding papers.
- Rigid baffle
 obliquity factor = 1.
obliquity factor = 1. - Soft baffle
 obliquity factor = cos(
obliquity factor = cos( ).
). - General baffle
 obliquity factor = cos(
obliquity factor = cos( )/(cos(
)/(cos( ) +
) + 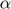 ), with
), with 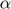 = (medium impedance)/(baffle impedance).
= (medium impedance)/(baffle impedance).
References for baffle models:
- Selfridge et al. A theory for the radiation pattern of a narrow-strip acoustic transducer. Appl Phys Lett 37(1), 35-36 (1980)
- Pesqué et al. Effect of the planar baffle impedance in acoustic radiation of a phased array element theory and experimentation. IEEE Ultrasonics Symposium, (1984)
Example: For a baffle of impedance 2.8 MRayl (epoxy) adjacent to soft tissues of impedance 1.6 MRayls, 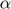 = 1.75.
= 1.75.
Note on CHIRP signals
Linear chirps are characterized by PARAM.TXnow, PARAM.fc and PARAM.TXfreqsweep. The transmitted pulse has a duration of approximately T (= PARAM.TXnow/PARAM.fc), with the amplitude and phase defined over the time interval -T/2 to +T/2.
The total frequency sweep is DeltaF (= PARAM.TXfreqsweep): the frequencies increase linearly from (PARAM.fc - DeltaF/2) to (PARAM.fc + DeltaF/2) in the defined time interval.
Documentation: Chirp spectrum in Wikipedia.
Examples of pulse responses
Here are two examples of PFIELD-derived pulse responses:
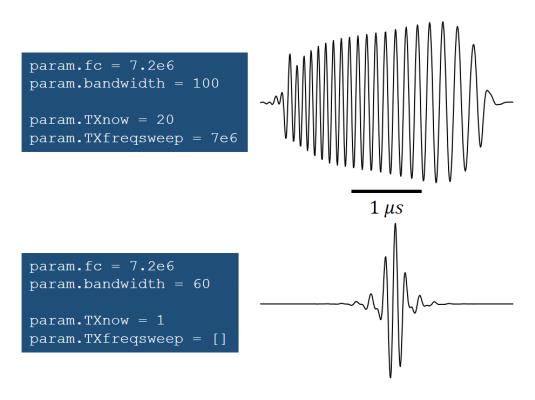
Advanced options
- FREQUENCY STEP & SAMPLES
Only frequency components of the transmitted signal in the range [0, 2fc] with significant amplitude are considered. The default relative amplitude is -100 dB in SIMUS. You can change this value by using the following:
[...] = SIMUS(...,OPTIONS),
where OPTIONS.dBThresh is the threshold in dB (default = -100).
The frequency step is determined automatically to avoid aliasing in the time domain. This step can be adjusted with a scaling factor OPTIONS.FrequencyStep (default = 1). It is not recommended to modify this scaling factor in SIMUS.
- FULL-FREQUENCY DIRECTIVITY
By default, the directivity of the elements depends on the center frequency only. This makes the algorithm faster. To make the directivities fully frequency-dependent, use:
[...] = SIMUS(...,OPTIONS),
with OPTIONS.FullFrequencyDirectivity = true (default = false).
- ELEMENT SPLITTING
Each transducer element of the array is split into small segments. The length of these small segments must be small enough to ensure that the far-field model is accurate. By default, the elements are split into M segments, with M being defined by:
M = ceil(element_width/smallest_wavelength);
To modify the number M of subelements by splitting, you may adjust OPTIONS.ElementSplitting. For example, OPTIONS.ElementSplitting = 1.
- WAIT BAR
If OPTIONS.WaitBar is true, a wait bar appears (only if the number of frequency samples >10). Default is true.
Example #1: RF signals using a phased-array transducer
This example shows how to simulate RF signals obtained with a focused wave generated by a cardiac phased-array transducer.
Download the properties of a 2.7-MHz 64-element cardiac phased array in a structure param by using GETPARAM.
param = getparam('P4-2v');
Choose a focus location at xf = 0 cm, zf = 5 cm.
xf = 0; zf = 5e-2; % focus position (in m)
Obtain the corresponding transmit time delays (in s).
txdel = txdelay(xf,zf,param); % in s
Define scatterers.
x = zeros(1,6); y = zeros(1,6); z = (1:2:11)*1e-2; % scatterers' positions RC = [ones(1,5) 0]; % reflection coefficients % The RC of the deepest scatterer is zero. It is a "ghost" scatterer, % which ensures that |SIMUS| simulates RF signals down to its location.
Check the pressure field with PFIELD.
[xi,zi] = impolgrid([256 128],11e-2,pi/3,param); % polar-type image grid yi = zeros(size(xi)); P = pfield(xi,yi,zi,txdel,param); pcolor(xi*1e2,zi*1e2,20*log10(P/max(P(:)))) shading interp colormap hot axis equal tight ij caxis([-20 0]) % dynamic range = [-20,0] dB c = colorbar; c.YTickLabel{end} = '0 dB'; xlabel('[cm]'), ylabel('[cm]') title('Wave focused at [0;5] cm') hold on plot(x(1:5)*1e2,z(1:5)*1e2,'ko','MarkerFaceColor','g') plot(x(6)*1e2,z(6)*1e2,'ko','MarkerFaceColor','w') hold off

Use a high sampling frequency to obtain RF signals with high temporal resolution (the default is 4 times the center frequency). It does not affect computational time.
param.fs = 20*param.fc; % sampling frequency
Simulate RF signal by using SIMUS.
RF = simus(x,y,z,RC,txdel,param);
Plot the RF signals.
plot((RF(:,1:7:64)/max(RF(:))+(1:10))',... (0:size(RF,1)-1)/param.fs*1e6,'k') set(gca,'XTick',1:10,'XTickLabel',int2str((1:7:64)')) title('RF signals') xlabel('Element number'), ylabel('time (\mus)') xlim([0 11]) axis ij square

Plot the RF signal acquired by the 32th element.
t = (0:size(RF,1)-1)/param.fs; % time (s) plot(t*1e6,RF(:,32)) set(gca,'YColor','none','box','off') xlabel('time (\mus)') title('RF signal acquired by the 32^{th} element') axis tight square

Magnify around the focus location.
c = 1540; % 1540 m/s is the default speed of sound tf = 2*5e-2/c; % 2-way time to focus point idx = abs(t-tf-txdel(32))<4/param.fc; plot(t(idx)*1e6,RF(idx,32),'LineWidth',2) set(gca,'YColor','none','box','off') xlabel('time (\mus)') title('RF signal acquired by the 32^{th} element (magnification)') axis tight square

Create a GIF movie named 'focusedWave.gif' with MKMOVIE.
param.movie = [5 10 30]; % 5-cm-by-10-cm ROI, resolution = 30 pix/cm mkmovie(x,z,RC,txdel,param,'focusedWave.gif');

Example #2: RF signals in plane wave imaging
This example shows how to simulate RF signals obtained with a plane wave generated by a linear array. The RF signals will be demodulated and beamformed to obtain a B-mode image.
Download the properties of a 7.6-MHz 128-element uniform linear array in a structure param by using GETPARAM.
param = getparam('L11-5v');
Generate 20 random scatterers.
n = 20;
x = rand(1,n)*3.8e-2-1.9e-2;
y = zeros(1,n);
z = rand(1,n)*3.5e-2+0.25e-2;
RC = 1/2+rand(1,n)/2; % reflection coefficients
Simulate RF signals by using SIMUS. The transmit delays are all zero to create an unsteered plane wave.
param.fs = 10*param.fc;
txdel = zeros(1,128); % null delays
RF = simus(x,y,z,RC,txdel,param);
Plot the RF signals.
RF = RF/max(abs(RF(:))); t = (0:size(RF,1)-1)/param.fs*1e6; % in microseconds plot((2*RF(:,1:6:128)+(1:22))',t,'b') set(gca,'XTick',1:3:22,'XTickLabel',int2str((1:18:128)')) title('RF signals') xlabel('Element number'), ylabel('time (\mus)') axis([0 23 0 t(end)]) axis ij square

Demodulate the RF signals to obtain I/Q signals
IQ = rf2iq(RF,param.fs,param.fc);
Plot the RF signal acquired by the 64th element and the corresponding I/Q.
RF64 = RF(:,64); IQ64 = IQ(:,64); % 64th signals p = max(abs(IQ64)); % peak plot(t,RF64/p+2,t,abs(IQ64)/p+2,t,real(IQ64)/p+1,t,imag(IQ64)/p) set(gca,'YColor','none','box','off') xlabel('time (\mus)') title('Signal acquired by the 64^{th} element') axis tight legend({'RF','|I/Q|','in-phase','quadrature'},... 'Location','NorthEastOutside')

Define a 256  256 image grid.
256 image grid.
xi = linspace(-2e-2,2e-2,256); % in m zi = linspace(0,4e-2,256); % in m [xi,zi] = meshgrid(xi,zi);
Beamform the I/Q signals by using DAS. Use a void f-number parameter. It will be determined automatically (and optimally).
param.fnumber = [];
IQb = das(IQ,xi,zi,txdel,param); % beamformed I/Q
Create and display a B-mode image.
B = bmode(IQb,30); % log-compressed image imagesc(xi(1,:)*1e2,zi(:,1)*1e2,B) c = colorbar; c.YTick = [0 255]; c.YTickLabel = {'-30 dB','0 dB'}; colormap gray axis equal tight xlabel('[cm]'), ylabel('[cm]') hold on plot(x*1e2,z*1e2,'ro','MarkerSize',10) hold off legend('Scatterers')

Example #3: M87-black-hole ultrasound image with diverging waves
This example shows how to simulate an ultrasound image with a series of circular waves generated by a cardiac phased array. The RF signals will be demodulated, beamformed, then merged to obtain a compound B-mode image.
Download the properties of a 2.7-MHz 64-element linear phased array in a structure param by using GETPARAM.
param = getparam('P4-2v');
Download an image of the supermassive M87 black hole.
I = imread(['https://static.projects.iq.harvard.edu/files/styles/',... 'os_files_xlarge/public/eht/files/20190410-78m-800x466.png']);
Simulate scatterers in a 12-cm-deep region.
Use GENSCAT to generate randomly distributed scatterers
depth = 10e-2; % in cm
[xs,~,zs,RC] = genscat([NaN depth],param,rgb2gray(I),0.4);
Display the scatterers
scatter(xs*1e2,zs*1e2,3,RC,'filled') axis equal ij tight colormap hot set(gca,'XColor','none','box','off') ylabel('[cm]') title('Scatterers and their reflection coefficients')

Simulate 21 sets of RF signals obtained with 21 circular waves tilted at different angles, beamform these signals onto a 128  128 polar grid, and obtain a compound I/Q dataset.
128 polar grid, and obtain a compound I/Q dataset.
tilt = linspace(-pi/4,pi/4,21); % tilt angles IQc = zeros(128,128,'like',1i); % will contain the compound I/Q opt.WaitBar = false; % no progress bar for SIMUS param.fs = param.fc*4; % RF sampling frequency [xI,zI] = impolgrid(128,10e-2,pi/2,param); % polar-type grid h = waitbar(0,'SIMUS & DAS...'); for k = 1:21 dels = txdelay(param,tilt(k),pi/2); % transmit delays RF = simus(xs,zs,RC,dels,param,opt); % RF simulation IQ = rf2iq(RF,param); % I/Q demodulation IQb = das(IQ,xI,zI,dels,param); % DAS beamforming IQc = IQc+IQb; % compounding waitbar(k/length(tilt),h,... ['SIMUS & DAS: ' int2str(k) ' of 21 completed']) end close(h)
Display the last ultrasound image (at 45-degree steering)
lcI = bmode(IQb,50); % log-compressed image pcolor(xI*1e2,zI*1e2,lcI) shading interp, axis equal ij tight c = colorbar; c.YTick = [0 255]; c.YTickLabel = {'-50 dB','0 dB'}; colormap gray axis equal tight ylabel('[cm]') set(gca,'XColor','none','box','off') colormap hot title('One ultrasound image (at +45 degrees)')

Display the M87-black-hole ultrasound compound image
lcI = bmode(IQc,50); % log-compressed image pcolor(xI*1e2,zI*1e2,lcI) shading interp, axis equal ij tight c = colorbar; c.YTick = [0 255]; c.YTickLabel = {'-50 dB','0 dB'}; colormap gray axis equal tight ylabel('[cm]') set(gca,'XColor','none','box','off') colormap hot title('M87-black-hole ultrasound compound image')

Display the original picture of the M87 black hole.
imshow(I,'InitialMagnification','fit') title('Supermassive black hole of M87')

Example #4: Recover a few scatterers with a convex array
This example shows how to simulate an ultrasound image with one circular wave generated by a curved linear array. The RF signals will be demodulated, then beamformed to obtain a B-mode image.
Download the properties of a 3.6-MHz 128-element convex array in a structure param by using GETPARAM.
param = getparam('C5-2v');
Design a few scatterers.
xs = [4.3 3.2 1.7 0 -1.7 -3.2 -4.3 0 -2.5 2.5]*1e-2; % in m zs = [7 8.1 8.8 9 8.8 8.1 7 5 2 2]*1e-2; % in m
Set all the transmit delays to 0.
txdel = zeros(1,param.Nelements);
Calculate and display the pressure field with PFIELD.
[x,z] = meshgrid(linspace(-.1,.1,256),linspace(0,.1,128)); P = pfield(x,z,txdel,param); imagesc(x(1,:)*1e2,z(:,1)*1e2,20*log10(P/max(P,[],'all'))) axis equal ij tight caxis([-20 0]) % dynamic range = [-20,0] dB c = colorbar; c.YTickLabel{end} = '0 dB'; colormap hot xlabel('x (cm)'), ylabel('z (cm)') title('Circular wave with a convex array') hold on plot(xs*1e2,zs*1e2,'bo','Linewidth',2) hold off legend('scatterers')

Simulate RF signals with SIMUS.
First add a "ghost" scatterer (its reflection coefficient is zero) at 10 cm deep to ensure that RF are simulated till 10-cm depth.
RC = [ones(1,numel(xs)) 0]; xs = [xs 0]; zs = [zs 1e-2]; RF = simus(xs,zs,RC,txdel,param);
Create a GIF movie named 'convexSmiley.gif' with MKMOVIE.
param.movie = [10 10 30]; % 10-cm-by-10-cm ROI, resolution = 30 pix/cm mkmovie(xs,zs,RC,txdel,param,'convexSmiley.gif');

Demodulate the RF signals with RF2IQ.
param.fs = 4*param.fc; % it is the default sampling frequency used by SIMUS
IQ = rf2iq(RF,param.fs,param.fc);
Display the hyperbolic signatures.
imagesc((0:size(RF,1))/param.fs*1e6,1:128,abs(IQ)) xlabel('element #') ylabel('time (\mus)') axis square title('Envelopes of the simulated RF signals')

Define a 256  512 image grid by using IMPOLGRID.
512 image grid by using IMPOLGRID.
[x,z] = impolgrid([256 512],0.1,param);
Beamform the I/Q signals onto this grid.
param.fnumber = []; % the f-number will be chosen automatically
IQb = das(IQ,x,z,txdel,param);
Display the resulting image with BMODE.
B = bmode(IQb,30); % B-mode image pcolor(x*1e2,z*1e2,B) shading interp axis equal ij tight c = colorbar; c.YTick = [0 255]; c.YTickLabel = {'-30 dB','0 dB'}; colormap gray xlabel('[cm]'), ylabel('[cm]') title('Circular wave imaging with a convex array')

See also
txdelay, impolgrid, genscat, simus3, pfield, mkmovie, cite
References
- The paper that describes the first 2-D version of PFIELD is: Shariari S, Garcia D. Meshfree simulations of ultrasound vector flow imaging using smoothed particle hydrodynamics. Phys Med Biol, 2018;63:205011. (PDF)
- The papers that describe the theory inside PFIELD and SIMUS are: Garcia D. SIMUS: an open-source simulator for medical ultrasound imaging. Part I: theory & examples. Comput Methods Programs Biomed, 2022. (PDF), and: Cigier A, Varray F, Garcia D. SIMUS: an open-source simulator for medical ultrasound imaging. Part II: comparison with four simulators. Comput Methods Programs Biomed, 2022. (PDF).
About the author
Damien Garcia, Eng., Ph.D. INSERM researcher Creatis, University of Lyon, France
websites: BioméCardio, MUST
Date modified