DAS3 Delay-And-Sum of volume (3-D) signals
DAS3 beamforms the RF or I/Q volume signals.
Contents
Syntax
BFSIG = DAS3(SIG,X,Y,Z,DELAYS,PARAM) beamforms the RF or I/Q signals stored in the array SIG, and returns the beamformed signals BFSIG. The signals are beamformed at the points specified by X, Y and Z.
TRY IT! Enter das3 in the command window for an example.
SIG must be a 2-D array. The first dimension (i.e. each column) corresponds to a single RF or I/Q signal over (fast-) time, with the COLUMN #n corresponding to the ELEMENT #n of PARAM.elements.
DELAYS are the transmit time delays (in s). The number of elements in DELAYS must be the number of elements in the array (which is equal to size(SIG,2)). If a sub-aperture was used during transmission, use DELAYS(i) = NaN if element # i of the linear array was off.
PARAM is a structure that contains the parameter values required for DAS beamforming (see below for details).
Note: SIG must be complex when beamforming I/Q data (i.e. SIG = complex(I,Q) = I + 1i*Q).
Note: DASMTX3
DAS3 calls DASMTX3. DASMTX3 creates a DAS matrix.
- Beamforming using DAS3: bfSIG = das3(SIG,x,y,z,delays,param)
- Beamforming using DASMTX3: M = dasmtx3(size(SIG),x,y,z,delays,param); bfSIG = M*SIG(:); bfSIG = reshape(bfSIG,size(x));
If you need to beamform a large series of ultrasound signals acquired with a same probe and a same transmit sequence, DASMTX3 is recommended. BEWARE, however. DASMTX3 can generate tall sparse DAS matrices when beamforming large volume data! Consider chunking your datasets.
DAS3 chunks the input data (X,Y,Z) automatically to avoid using too large matrices.
Other syntaxes
DAS3(SIG,X,Y,Z,PARAM) uses DELAYS = param.TXdelay.
DAS3(...,METHOD) specifies the interpolation method. The available methods are decribed in NOTE #3 below.
[M,PARAM] = DAS3(...) also returns the structure PARAM with the default values.
The structure PARAM
PARAM is a structure that contains the following fields:
- PARAM.fs: sampling frequency (in Hz, required)
- PARAM.elements: x- and y-coordinates of the element centers (in m, required). It MUST be a two-row matrix, with the 1st and 2nd rows containing the x and y coordinates, respectively.
- PARAM.fc: central frequency (in Hz, required for I/Q signals)
- PARAM.TXdelay: transmission law delays (in s, required if the vector DELAYS is not given)
- PARAM.c: longitudinal velocity (in m/s, default = 1540 m/s)
- PARAM.t0: start time for reception (in s, default = 0 s)
- PARAM.fnumber: reception f-number (default = [0 0], i.e. full aperture). PARAM.fnumber(1) = reception f-number in the azimuthal x-direction. PARAM.fnumber(2) = reception f-number in the elevation y-direction.
Passive imaging
PARAM.passive: must be true for passive imaging (i.e. no transmit). The default is false.
Notes
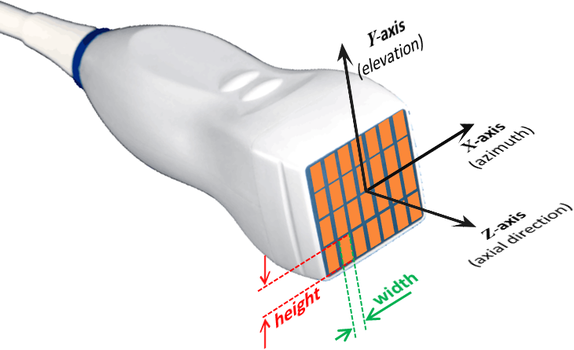
- NOTE #1: X-, Y-, and Z-axes
Conventional axes are used:
The X-axis is PARALLEL to the transducer. The Z-axis is PERPENDICULAR to the transducer and points downward (Z = 0 at the level of the transducer, Z increases as depth increases). The Y-axis is such that the coordinates are right-handed. These axes are represented in the following figure.
- NOTE #2:
DAS3 uses a standard delay-and-sum. Phase rotations are included if I/Q (complex) signals are beamformed.
- NOTE #3: interpolation methods
By default DAS3 uses a linear interpolation. To specify the interpolation method, use DAS3(...,METHOD), with METHOD being:
- 'nearest' : nearest neighbor interpolation
- 'linear' : (default) linear interpolation
- 'quadratic' : quadratic interpolation
- 'lanczos3' : 3-lobe Lanczos (windowed sinc) interpolation
- '5points' : 5-point least-squares parabolic interpolation
- 'lanczos5' : 5-lobe Lanczos (windowed sinc) interpolation
The linear interpolation (it is a 2-point method) returns a matrix twice denser than the nearest-neighbor interpolation. It is 3, 4, 5, 6 times denser for 'quadratic', 'lanczos3', '5points', 'lanczos5', respectively (they are 3-to-6-point methods).
Example: Two-way PSF for a focused wave by a 32x32 matrix array
This example shows how to simulate RF signals then beamform I/Q signals
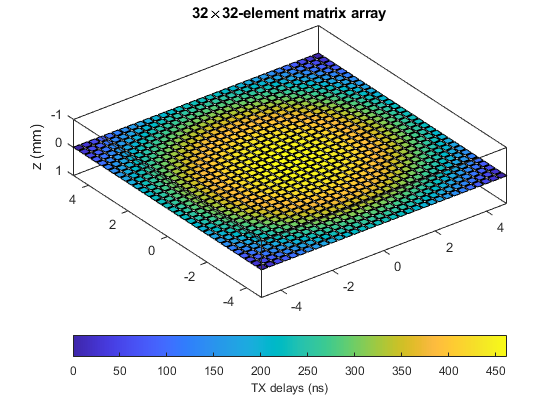
Create a 3-MHz matrix array with 32x32 elements.
param = []; param.fc = 3e6; param.bandwidth = 70; param.width = 250e-6; param.height = 250e-6;
Specify the x- and y-coordinates of the elements.
pitch = 300e-6; % pitch (in m)
[xe,ye] = meshgrid(((1:32)-16.5)*pitch);
param.elements = [xe(:).'; ye(:).'];
Use TXDELAY3 to calculate the transmit delays for a focused wave.
x0 = 0; y0 = 0; z0 = 3e-2; txdel = txdelay3(x0,y0,z0,param);
Plot the transducer with VIEWXDCR.
p = viewxdcr(param); p.FaceVertexCData = txdel(:)*1e9; title('32\times32-element matrix array') c = colorbar('SouthOutside'); c.Label.String = 'TX delays (ns)';
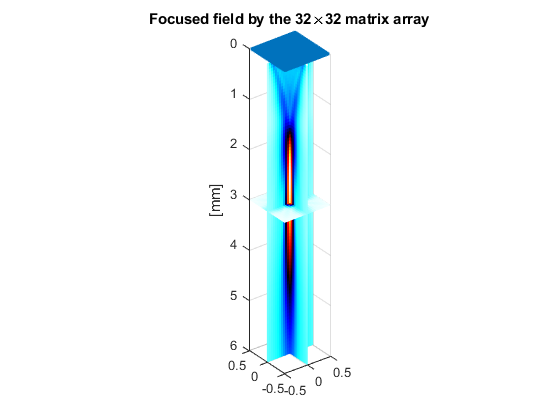
Calculate the pressure field with PFIELD3.
n = 24;
[xi,yi,zi] = meshgrid(linspace(-5e-3,5e-3,n),linspace(-5e-3,5e-3,n),...
linspace(0,6e-2,4*n));
RP = pfield3(xi,yi,zi,txdel,param);
Have a look at the RMS pressure field.
figure slice(xi*1e2,yi*1e2,zi*1e2,RP,0,0,3) set(gca,'zdir','reverse') zlabel('[mm]') shading flat axis equal colormap([1-hot;hot]) hold on plot3(xe(:)*1e2,ye(:)*1e2,0*xe(:),'.') title('Focused field by the 32{\times}32 matrix array')
Simulate RF signals by using SIMUS3.
[RF,param] = simus3(x0,y0,z0,1,txdel,param);
Demodulate the RF signals with RF2IQ.
IQ = rf2iq(RF,param);
Create a 3-D grid for beamforming.
lambda = 1540/param.fc;
[xi,yi,zi] = meshgrid(-2e-2:lambda:2e-2,-2e-2:lambda:2e-2,...
2.5e-2:lambda/2:3.2e-2);
Beamform the I/Q signals with DAS3.
IQb = das3(IQ,xi,yi,zi,txdel,param);
Obtain the log-envelope.
env = abs(IQb); I = 20*log10(env/max(env(:)));
Display the two-way PSF.
figure I(1:round(size(I,1)/2),1:round(size(I,2)/2),:) = NaN; for k = [-40:10:-10 -5 -1] isosurface(xi*1e2,yi*1e2,zi*1e2,I,k) end view(-60,40) colormap([1-hot;hot]) c = colorbar; c.Label.String = 'dB'; box on, grid on zlabel('[cm]') title('PSF at the focal point [dB]')

See also
cite, das, dasmtx3, simus3, txdelay3
References
- Perrot V, Polichetti M, Varray F, Garcia D. So you think you can DAS? A viewpoint on delay-and-sum beamforming. Ultrasonics, 2021; 111:106309. (PDF)
About the author
Damien Garcia, Eng., Ph.D. INSERM researcher Creatis, University of Lyon, France
websites: BioméCardio, MUST
Date modified