SIMUS3 Simulation of ultrasound RF signals for a planar 2-D array

SIMUS3 simulates ultrasound RF radio-frequency signals generated by an ultrasound planar 2-D array insonifying a medium of scatterers.

Contents

Syntax

RF = SIMUS3(X,Y,Z,RC,DELAYS,PARAM) simulates ultrasound RF radio- frequency signals generated by an ultrasound planar 2-D array insonifying a medium of scatterers. The scatterers are characterized by their coordinates (X, Y, Z) and reflection coefficients RC.

X, Y, Z and RC must be of same size. The elements of the 2-D array are excited at different time delays, given by the vector DELAYS. The transmission and reception characteristics must be given in the structure PARAM (see below for details).

TRY IT! Enter simus3 in the command window for an example.

The RF output matrix contains Number_of_Elements columns. Each column therefore represents an RF signal. The number of rows depends on the depth (estimated from max(Z)) and the sampling frequency PARAM.fs (see below). By default, the sampling frequency is four times the center frequency.

Units: X, Y, Z must be in m; DELAYS must be in s; RC has no unit. RF has arbitrary unit.

DELAYS can also be a matrix. This alternative can be used to simulate MPT (multi-plane transmit) sequences. In this case, each ROW represents a delay series. For example, to create a 4-MPT sequence with a 1024-element phased array, DELAYS matrix must have 4 rows and 1024 columns (size = [4 1024]).

SIMUS3 uses PFIELD3 during transmission and reception. The parameters that must be included in the structure PARAM are similar as those in PFIELD3. Additional parameters are also required (see below).

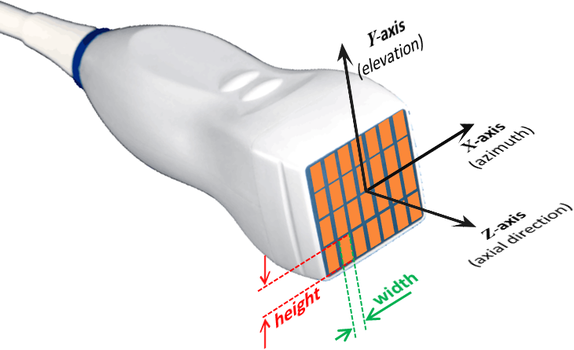
Planar 2-D array

The present version of SIMUS3 only considers planar 2-D array whose z-coordinates of the elements are 0. All the elements are rectangular and have equal width and height.

The element width and height are both required as input parameters for SIMUS3. The element See the paragraph below entitled The structure PARAM for details.

The structure PARAM

PARAM is a structure that contains the following fields:

Other syntaxes

[RP,PARAM] = SIMUS3(...) also returns the complete list of parameters including the default values.

[...] = SIMUS3 without any input argument provides an example designed to produce RF signals from a focused ultrasound beam using a 3 MHz matrix array transducer.

Parallel computing

SIMUS3 calls the function PFIELD3. If you have the Parallel Computing Toolbox, SIMUS3 can run several PFIELD3 functions in parallel. If this option is activated, a parallel pool is created on the default cluster. All workers in the pool are used. The X, Y and Z are split into Nw chunks, Nw being the number of workers. To execute parallel computing, use:

[...] = SIMUS3(...,OPTIONS),

with OPTIONS.ParPool = true (default = false).

X-, Y-, and Z-axes

Conventional axes are used:

The X-axis is PARALLEL to the transducer. The Z-axis is PERPENDICULAR to the transducer and points downward (Z = 0 at the level of the transducer, Z increases as depth increases). The Y-axis is such that the coordinates are right-handed. These axes are represented in the above figure.

Element directivity

By default, the calculation is made faster by assuming that the directivity of the elements is dependent only on the central frequency (see figure below). This simplification very little affects the pressure field in most situations (except in the vicinity of the array). To turn off this option, use OPTIONS.FullFrequencyDirectivity = true.

See ADVANCED OPTIONS below.

Present version of SIMUS3

The present version of SIMUS3 only considers planar 2-D array whose z-coordinates of the elements are 0. All the elements are rectangular and have equal width and height.

SIMUS vs. SIMUS3

PFIELD and SIMUS use 2-D or 3-D linear acoustic equations depending on the input parameters. With PFIELD or SIMUS, a 3-D method is used to account for elevation focusing. The transmit delays in the Y direction cannot be adjusted as needed; only the elevation focal length can be modified. For more general 3-D cases, it is necessary to use PFIELD3 or SIMUS3.

Note on CHIRP signals

Linear chirps are characterized by PARAM.TXnow, PARAM.fc and PARAM.TXfreqsweep. The transmitted pulse has a duration of approximately T (= PARAM.TXnow/PARAM.fc), with the amplitude and phase defined over the time interval -T/2 to +T/2.

The total frequency sweep is DeltaF (= PARAM.TXfreqsweep): the frequencies increase linearly from (PARAM.fc - DeltaF/2) to (PARAM.fc + DeltaF/2) in the defined time interval.

Documentation: Chirp spectrum in Wikipedia.

Advanced options

Only frequency components of the transmitted signal in the range [0, 2fc] with significant amplitude are considered. The default relative amplitude is -100 dB in SIMUS3. You can change this value by using the following:

[...] = SIMUS3(...,OPTIONS),

where OPTIONS.dBThresh is the threshold in dB (default = -100).

The frequency step is determined automatically to avoid aliasing in the time domain. This step can be adjusted with a scaling factor OPTIONS.FrequencyStep (default = 1). It is not recommended to modify this scaling factor in SIMUS3.

By default, the directivity of the elements depends on the center frequency only. This makes the algorithm faster. To make the directivities fully frequency-dependent, use:

[...] = SIMUS3(...,OPTIONS),

with OPTIONS.FullFrequencyDirectivity = true (default = false).

Each transducer element of the array is split into small rectangles. The width and height of these small rectangles must be small enough to ensure that the far-field model is accurate. By default, the elements are split into M-by-N rectangles, with M and N being defined by:

M = ceil(element_width/smallest_wavelength);

N = ceil(element_height/smallest_wavelength);

To modify the number MN of subelements by splitting, you may adjust OPTIONS.ElementSplitting, which must contain two elements. For example, OPTIONS.ElementSplitting = [1 3].

If OPTIONS.WaitBar is true, a wait bar appears (only if the number of frequency samples >10). Default is true.

Example: Two-way PSF for a focused wave by a 32x32 matrix array

This example shows how to simulate RF signals then beamform I/Q signals

Create a 3-MHz matrix array with 32x32 elements.

param = [];
param.fc = 3e6;
param.bandwidth = 70;
param.width = 250e-6;
param.height = 250e-6;

Specify the x- and y-coordinates of the elements.

pitch = 300e-6; % pitch (in m)
[xe,ye] = meshgrid(((1:32)-16.5)*pitch);
param.elements = [xe(:).'; ye(:).'];

Use TXDELAY3 to calculate the transmit delays for a focused wave.

x0 = 0; y0 = 0; z0 = 3e-2;
txdel = txdelay3(x0,y0,z0,param);

Plot the transducer with VIEWXDCR.

p = viewxdcr(param);
p.FaceVertexCData = txdel(:)*1e9;
title('32\times32-element matrix array')
c = colorbar('SouthOutside');
c.Label.String = 'TX delays (ns)';

Calculate the pressure field with PFIELD3.

n = 24;
[xi,yi,zi] = meshgrid(linspace(-5e-3,5e-3,n),linspace(-5e-3,5e-3,n),...
    linspace(0,6e-2,4*n));
RP = pfield3(xi,yi,zi,txdel,param);

Have a look at the RMS pressure field.

figure
slice(xi*1e2,yi*1e2,zi*1e2,RP,0,0,3)
set(gca,'zdir','reverse')
zlabel('[mm]')
shading flat
axis equal
colormap([1-hot;hot])
hold on
plot3(xe(:)*1e2,ye(:)*1e2,0*xe(:),'.')
title('Focused field by the 32{\times}32 matrix array')

Simulate RF signals by using SIMUS3.

[RF,param] = simus3(x0,y0,z0,1,txdel,param);

Demodulate the RF signals with RF2IQ.

IQ = rf2iq(RF,param);

Create a 3-D grid for beamforming.

lambda = 1540/param.fc;
[xi,yi,zi] = meshgrid(-2e-2:lambda:2e-2,-2e-2:lambda:2e-2,...
    2.5e-2:lambda/2:3.2e-2);

Beamform the I/Q signals with DAS3.

IQb = das3(IQ,xi,yi,zi,txdel,param);

Obtain the log-envelope.

env = abs(IQb);
I = 20*log10(env/max(env(:)));

Display the two-way PSF.

figure
I(1:round(size(I,1)/2),1:round(size(I,2)/2),:) = NaN;
for k = [-40:10:-10 -5 -1]
    isosurface(xi*1e2,yi*1e2,zi*1e2,I,k)
end
view(-60,40)
colormap([1-hot;hot])
c = colorbar;
c.Label.String = 'dB';
box on, grid on
zlabel('[cm]')
title('PSF at the focal point [dB]')

See also

cite, das3, pfield3, simus, txdelay3

References

About the author

Damien Garcia, Eng., Ph.D.
INSERM researcher
Creatis, University of Lyon, France

websites: BioméCardio, MUST

Date modified

Published with MATLAB® R2022a